Prva vježba: geometrija dvaju pogleda

Mnoge metode računalnog vida razmatraju rekonstrukciju geometrije više pogleda gdje je na temelju više pogleda na scenu potrebno izlučiti relativnu orijentaciju kamera i rekonstruirati trodimenzionalnu strukturu scene. Vrlo važan specijalni slučaj razmatra jednu kameru koja se giba kroz scenu koja se sastoji od pokretnih objekata i nepokretne pozadine. U tom slučaju možemo pričati o izlučivanju strukture iz kretanja (eng. structure from motion).

Cilj ove vježbe je uhodati osnovni postupak za procjenu relativne orijentacije kamera te procijeniti doprinos Hartleyeve normalizacije. Eksperimente ćemo provoditi na sintetičkim podatcima kako bismo izbjegli potrebu za mjerenjem točnog pomaka kamera. Započet ćemo s pregledom osnovnih pojmova, zatim uvesti eksperimentalni postav i opisati elemente postupka procjene, objasniti mjere točnosti te na kraju opisati zadatke od kojih se ova vježba sastoji.

Stvaranje slike

Složenost rekonstrukcijskih postupaka jako ovisi o dostupnosti intrinsičnih parametara kamere zato što ti parametri omogućavaju povezivanje piksela s orijentiranim poluzrakama u koordinatnom sustavu kamere. Ako su intrinsični parametri poznati, geometriju više pogleda možemo rekonstruirati sve do nepoznatog faktora globalnog mjerila. U suprotnom, rekonstrukciju možemo provesti samo do nepoznate projekcijske transformacije.

Radi jednostavnosti, u ovoj vježbi pretpostavit ćemo da su intrinsični parametri poznati jer je taj slučaj najvažniji u praksi. U tom slučaju elemente slikovne ravnine možemo predstaviti u normaliziranim koordinatama. Neka se točka 3D prostora \(\mathbf{Q}=(X_Q, Y_Q, Z_Q)\) preslikava u slikovni element \(\mathbf{q}\) čije su normalizirane koordinate \((x_q, y_q)\). Ako je točka \(Q\) izražena u koordinatnom sustavu kamere, tada normalizirane slikovne koordinate odgovaraju tangensima kutova koji definiraju zraku (\(\mathbf{Q}, \mathbf{q}\)):

Ako obje točke predstavimo projekcijskim koordinatama, tada imamo \(\mathbf{Q}=(X_Q, Y_Q, Z_Q, 1)\) te \(\mathbf{q}=(x_q, y_q, 1)\). Primijetite da koristimo iste nazive točaka kao i u euklidskom slučaju jer je značenje jasno iz konteksta. Stoga projekciju možemo opisati sljedećom linearnom jednadžbom:

Promotrimo 3D točku \(\mathbf{Q}_W\) zadane u proizvoljnom koordinatnom sustavu W. Sada tu točku možemo prikazati u koordinatnom sustavu kamere primjenom odgovarajuće transformacije krutog tijela definirane rotacijskom matricom \(\mathbf{R}\) te vektorom \(\mathbf{T}\):

Lako se pokaže da se projekcija točke \mathbf{Q}_W na slikovnu ravninu može opisati sljedećom linearnom jednadžbom:

Relativna orijentacija

Pretpostavimo da su zadane kamere A i B koje promatraju istu scenu. Označimo 3D točke u sustavu kamere A s \(\mathbf{Q}_A\) te 3D točke u sustavu kamere B s \(\mathbf{Q}_B\). Tada postoje rotacijska matrica \(\mathbf{R}\) te vektor \(\mathbf{T}\) za koje vrijedi:

Kažemo da transformacija krutog tijela (\(\mathbf{R}\), \(\mathbf{T}\)) određuje relativnu orijentaciju kamera A i B. Sve metode 3D rekonstrukcije u prvom koraku izlučuju relativnu orijentaciju dvaju kamera pa ćemo upravo taj zadatak razmatrati i u ovoj vježbi. Zadatak ćemo rješavati pod pretpostavkom da je koordinatni sustav svijeta poravnat s koordinatnim sustavom prve kamere. Ta pretpostavka neće smanjiti općenitost rješenja. Stoga, projekcijska matrica prve kamere biti će \(\mathbf{P}_a = \left\lbrack \mathbf{I} | \mathbf{0} \right\rbrack\), dok će naš postupak trebati izlučiti projekcijsku matricu druge kamere \(\mathbf{P}_b = \left\lbrack \mathbf{R} | \mathbf{t} \right\rbrack\).

Valja napomenuti da će svi naši postupci moći izlučiti samo smjer translacije ali ne i njen iznos. Razlog tome je nemogućnost razlikovanja iznosa translacije od globalnog mjerila trodimenzionalne rekonstrukcije scene. Drugim riječima, ako umjesto prave scene promatramo \(s\times\) umanjenu maketu te s jednakim faktorom \(s\) umanjimo i pomak druge kamere - dobit ćemo iste slike kao i u početnom slučaju. Zbog toga translacijsku komponentu relativne orijentacije obično izražavamo jediničnim vektorom te označavamo s \(\mathbf{t}\). Ova činjenica često koristi pri snimanju filmova. Slika pokazuje minijaturnu repliku Hogwartsa koja je korištena za snimanje filmova o Harryju Potteru. Jasno je da su takve minijature puno jeftinije od odgovarajuće scenografije u prirodnoj veličini!

Triangulacija strukture

Pretpostavimo za trenutak da smo uspjeli izlučiti relativnu orijentaciju te da želimo rekonstruirati trodimenzionalnu strukturu scene. Dakle, poznate su projekcijske matrice obje kamere, \(\mathbf{P}_a\) i \(\mathbf{P}_b\) te korespondentne točke \(\mathbf{q}_{a}\) i \(\mathbf{q}_{b}\), a naš zadatak je odrediti 3D položaj \(\mathbf{Q}\).

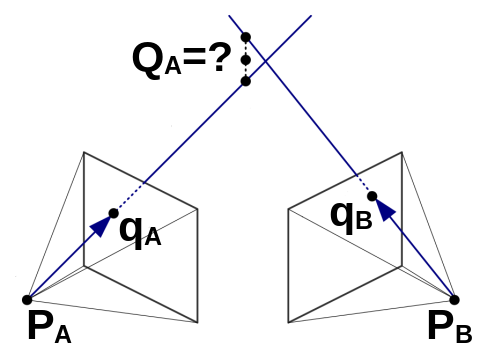
Slika pokazuje da je općeniti slučaj triangulacije znatno teži od stereoskopskog određivanja dubine. Poluzrake koje odgovaraju korespondentnim pikselima u prisustvu šuma neće biti koplanarne (szeliski22book, 11.2.4). Stoga tražimo rekonstrukciju koja se ne nalazi na niti jednoj od dviju zraka. Najmanje netočna bila bi ona rekonstrukcija čija reprojekcija bi bila najmanje udaljena od izmjerenih položaja korespondentnih točaka. Međutim, takav postupak zahtijevao bi nelinearnu združenu optimizaciju svih rekonstruiranih točaka zajedno s dvjema projekcijskim matricama (engels06isprs). Za potrebe ove vježbe zadovoljit ćemo se s jednostavnijim rješenjem koje dobro funkcionira u praksi.

Problemu možemo pristupiti na način da primijetimo da su ograničenja linearna u svim nepoznanicama. Ako se točka \(\mathbf{Q}\) u koordinatnom sustavu svijeta preslikava u točke \(\mathbf{q}_a\) i \(\mathbf{q}_b\), onda vrijede sljedeće jednadžbe:

Poznate vrijednosti su \(\mathbf{q}_a\), \(\mathbf{q}_b\), \(\mathbf{P}_a\) i \(\mathbf{P}_b\), a želimo naći \(\mathbf{Q}\). Nepoznate multiplikativne faktore \(\lambda_a\) i \(\lambda_b\) možemo izbaciti iz igre na način da obje strane vektorski pomnožimo s odgovarajućom točkom slike. Tako dobivamo linearni sustav u kojem svaka kamera doprinosi dva linearno nezavisna ograničenja:

\(\mathbf{q}_c \times (\mathbf{P}_c \cdot \mathbf{Q})=\mathbf{0}, \quad c \in{a,b}\).

Kad raspišemo sve četiri jednadžbe, dobivamo homogeni linearni sustav s četiri jednadžbe i četiri nepoznanice:

Standardan pristup za rješavanje ovakvih sustava temelji se na singularnoj dekompoziciji. Preciznije, netrivijalno rješenje sustava koje minimizira algebarski rezidual odgovara desnom singularnom vektoru matrice \(\mathbf{M}\) koji odgovara njenoj najmanjoj singularnoj vrijednosti.

Sintetički eksperimentalni postav

Metode relativne orijentacije teško je vrednovati na stvarnim slikama zbog kompliciranog mjerenja stvarnog pomaka između dvije kamere. Zbog toga ćemo ovu vježbu provoditi na sintetičkom eksperimentalnom postavu gdje dvije kamere promatraju slučajni oblak točaka. Radi jednostavnosti, obje kamere nalaze se u ravnini x-z referentne kamere, a udaljenost među ishodištima kamera uvijek ima jediničnu normu. Stoga pomak druge kamere nedvosmisleno možemo opisati pomakom smjera gledanja druge kamere te orijentacijom spojnice dvaju ishodišta. Oblak točaka instanciramo u kvadru za kojeg zadajemo udaljenost od referentne kamere i dubinu. Sljedeća slika ilustrira navedene parametre i prikazuje tri konkretne konfiguracije:

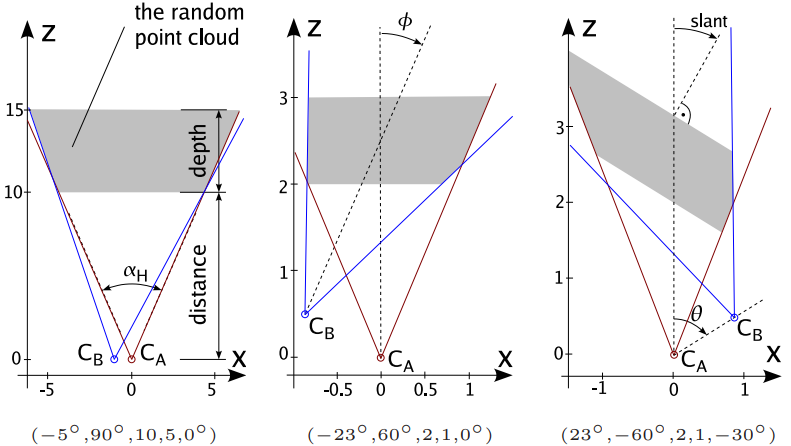
Slika ilustrira i kako se oblak točaka instancira samo u dijelovima scene koji su vidljivi u obje kamere (pinz07bencos). Da bismo to mogli provesti, potrebni su nam intrinsični parametri kamera (pretpostavljamo da obje kamere imaju iste parametre). Konačno, kako bismo izmjerili otpornost metode na šum, svakoj projiciranoj točci dodajemo slučajan normalni šum varijance \(\sigma\).

Eksperimentalni postav zadajemo sljedećim parametrima od kojih su mnogi označeni i na prethodnoj slici:

• \(\phi\): smjer gledanja kamere C_B u odnosu na referentnu kameru C_A (stupnjevi)
• \(\theta\): smjer pomaka kamere C_B u odnosu na referentnu kameru C_A (stupnjevi)
• \(D\): udaljenost oblaka točaka,
• \(d\): dubina oblaka točaka,
• \(\delta\): nagib oblaka točaka,
• \(N\): broj točaka.
• \(\alpha_H\): horizontalno vidno polje u stupnjevima,
• w, h: dimenzije slike,
• \(\sigma\): standardna devijacija šuma u pikselima.

Eksperimentalni postav možemo instancirati primjenom sljedećeg programa. Program bi se trebao moći prevesti s bilo kojim standardnim prevoditeljem (mi smo testirali g++ i MSVC). Javite ako bude bilo bilo kakvih problema. Parametri postava zadaju se u naredbenom retku. Evo primjera naredbenog retka koji instancira postav na lijevoj slici:

./create_2vg_setup -5_90_10_5_0_10000 45_384_288_100 >exp.data

Navedeni primjer zadaje \(\phi=-5^\circ\), \(\theta=90^\circ\), \(D=10\), \(d=5\), \(\delta=0\), \(N=10000\), \(\alpha_H\)=\(45^\circ\), w,h=384,288, \(\sigma=1.00\). Primijetite da zbog lakšeg parsanja, program zahtijeva da sve parametre upišemo kao cjelobrojne konstante te da se zadaje standardna devijacija pomnožena sa 100. Ako za prvi argument zadamo xx, smjer gledanja druge kamere odabrat će se tako da presjecište smjerova gledanja bude u sredini oblaka točaka. Evo primjera:

./create_2vg_setup xx_00_10_5_0_10000 45_384_288_100 >exp.data

Program za kreiranje postava ispisuje projekcijsku matricu druge kamere te dva polja po N projiciranih točaka za dvije kamere pretpostavljenog postava. Pojedini elementi ispisa razdvojeni su praznim retkom. U svim prikazanim primjerima, ispis programa preusmjerava se u datoteku exp.data, ali u praksi, ako program pokrećemo iz naredbenog retka, možemo koristiti i ulančavanje procesa. Matricu kamere P te vektore točaka qas i qbs iz Pythona možemo čitati sljedećim kodom:

import numpy as np
import itertools
import sys

def makegen(f):
  return ( np.array([float(c) 
    for c in line[1:-2].split(',')])
      for line in itertools.takewhile(lambda x: x != "\n", f))

# f = open('exp.data')
f = sys.stdin
line = f.readline().split('),(')
line[0] = line[0][7:]
line[2] = line[2][:-3]
P = np.array([ [float(x)  for x in row.split(',')] for row in line])
f.readline()

qas = np.array(list(makegen(f)))
qbs = np.array(list(makegen(f)))

Algoritam s osam točaka

Algoritam s osam točaka temelji se na epipolarnom ograničenju koje možemo zapisati kao bilinearnu formu nad homogenim prikazima korespondentnih točkaka \(\mathbf{q}_{ia} = (x_{ia}, y_{ia}, 1)\) i \(\mathbf{q}_{ib} = (x_{ib}, y_{ib}, 1)\) te nepoznatom esencijalnom matricom \(\mathbf{E}\):

Podsjetimo se, epipolarno ograničenje kaže da su prikazi točke \(\mathbf{Q}\) u koordinatnim sustavima dvaju kamera koplanarni sa spojnicom dvaju žarišta. Epipolarno ograničenje možemo presložiti tako da 9 parametara matrice \(\mathbf{E}\) istaknemo kao nepoznanice te ga zapisati u homogenom matričnom obliku kako slijedi:

Ako prikupimo n korespondencija, dobit ćemo homogeni linearni sustav s viškom ograničenja koji rješavamo standardnom metodom (SVD):

Primijetimo da ovaj algoritam ne bismo mogli prikazati u zatvorenom obliku kad korespondencije ne bi bile zapisane u homogenom prikazu.

Dekompozicija esencijalne matrice

Matrica koju smo dobili rješavanjem homogenog linearnog sustava ima 8 stupnjeva slobode. Međutim, mi znamo da esencijalna matrica ima samo 5 stupnjeva slobode jer vrijedi: \(\mathbf{E} = [\mathbf{t}]_\times \mathbf{R}\). Nadalje, mi znamo da matrica \(\mathbf{E}\) nema puni rang, jer epipolarno ograničenje degenerira u epipolovima (epipol je projekcija žarišta druge kamere):

Zbog toga ćemo izlučenu matricu “približiti” mnogostrukosti esencijalnih matrica kako slijedi. Prvo ćemo provesti singularnu dekompoziciju procijenjene esencijalne matrice:

Nakon toga, po potrebi ćemo matrice U i V pomnožiti s -1 tako da njihova determinanta bude pozitivna i jednaka 1. To možemo provesti bez smanjenja općenitosti jer matrice \(\mathbf{E}\) i \(-\mathbf{E}\) odgovaraju istoj epipolarnoj geometriji. Nastavak postupka implicitno će matricu singularnih vrijednosti postaviti na \(\mathbf{D}' = \mathrm{diag}(1,1,0)\) i rekombinirati faktore (nister04pami).

Sada možemo formulirati postupak dekompozicije esencijalne matrice na faktore pomaka druge kamere \(\mathbf{R}\) i \(\mathbf{t}\). Neka je zadana singularna dekompozicija korigirane esencijalne matrice:

Tada pomak druge kamere odgovara trećem lijevom singularnom vektoru:

Nadalje, dobivamo dvije hipoteze za rotacijsku matricu:

Moramo uzeti u obzir da translacijski pomak može biti negativan i pozitivan pa konačno dobivamo četiri hipoteze:

• (\(\mathbf{R}_a\), \(\mathbf{t}\)),
• (\(\mathbf{R}_a\), \(-\mathbf{t}\)),
• (\(\mathbf{R}_b\), \(\mathbf{t}\)),
• (\(\mathbf{R}_b\), \(-\mathbf{t}\))

Odabir točne hipoteze provodimo trianguliranjem korespondencija. Pobjeđuje ona hipoteza za koju se najveći broj rekonstrukcija nalazi ispred obje kamere. Potrebno je formirati dvije projekcijske matrice, \(\mathbf{P}_a = [\mathbf{I}|\mathbf{0}]\) i \(\mathbf{P}_b\) prema hipotezi, triangulirati strukturu \(\mathbf{Q}_{ia}\), prebaciti je u koordinate druge kamere (\(\mathbf{Q}_{ib}\)), odrediti Euklidski prikaz (\(\mathbf{Q}^E_{ia}\) i \(\mathbf{Q}^E_{ib}\)), te pobrojati broj korespondencija za koje je i \(Q^E_{iaz}>0\) i \(Q^E_{ibz}>0\).

Normalizacija koordinata korespondencija

Kod tipičnih kamera, širina vidnog polja manja je od \(\pi\)/2, a to znači da su normalizirane koordinate vidljivih točaka manje od 1. Stoga će linearni članovi homogenog sustava algoritma s osam točaka imati znatno veći šum od kvadratnih. Posljedično, optimizacija će biti sklona “smanjiti” elemente esencijalne matrice koji odgovaraju linearnim članovima (pinz07bencos). Ovom problemu možemo doskočiti ako primijetimo da epipolarnu estimaciju možemo provesti i nad linearno transformiranim korespondencijama. Označimo transformirane korespondencije s \(\mathbf{q}'_{ia}\) i \(\mathbf{q}'_{ib}\) tako da vrijedi:

Prikladno kondicioniranje linearnog sustava možemo postići na način da matrice \(\mathbf{T}_a\) i \(\mathbf{T}_b\) u obje slike postavimo prema sljedećem kriteriju. Transformacijske matrice treba konstruirati tako da težište transformiranih točaka bude u ishodištu te da njihova prosječna udaljenost od ishodišta bude \(\sqrt{2}\) (hartley97pami).

Pretpostavimo da smo za transformirane korespondencije riješili epipolarnu geometriju algoritmom s osam točaka odnosno da smo izlučili matricu \(\mathbf{F}\) za koju vrijedi:

Napominjemo da \(\mathbf{F}\) nije esencijalna matrica jer transformirane korespondencije nisu izražene u normaliziranom koordinatnom sustavu slike. Sada uvrštanjem izraza za \(\mathbf{q}'_{ia}\) i \(\mathbf{q}'_{ib}\) dobivamo:

Druga jednakost vrijedi zbog asocijativnosti matričnog množenja. Sada je jasno da tražena esencijalna matrica odgovara jednostavnoj transformaciji matrice \(\mathbf{F}\) koja je rješenje prikladno kondicioniranog homogenog sustava dobivenog iz transformiranih korespondencija:

Procjena pogreške

Obično se u literaturi odvojeno prikazuju pogreške u rotaciji i translaciji. Rotacijska pogreška odgovara rotacijskoj matrici koja ispravlja našu procjenu. Neka je \(\mathbf{R}\) - točna rotacijska matrica koju smo zadali u našem sintetičkom eksperimentalnom postavu te neka je \(\hat{\mathbf{R}}\) - naša procjena. Tada korekcijsku matricu \(\mathbf{R}_e\) možemo izračunati kao:

Konačno, mjeru pogreške možemo procijeniti kao rotacijski kut koji odgovara korekcijskoj matrici:

Podsjetimo se, translaciju je moguće procijeniti samo do na nepoznati multiplikativni faktor. Zato translacijsku pogrešku tipično procjenjujemo kutem između normalizirane točne translacije i naše procjene svedene na jediničnu normu:

Pokazuje se da su rotacijske pogreške znatno manje od translacijskih. Zbog toga točnost postupaka za procjenu relativne orijentacije tipično kvantificiramo translacijskom pogreškom \(\epsilon_T\).

Zadatci

U ovoj vježbi usredotočit ćemo se na sljedeće konfiguracije:

• deset različitih pomaka: \(\theta \in [0, 10, 20, ..., 90]\) (stupnjevi)
• konvergentni kutevi gledanja: \(\phi\) = 'xx'
• (D,d,\(\delta\)) = (10,5,0)
• ukupni broj točaka volumena: N = 10000
• uobičajena širina vidnog polja: \(\alpha_H\) = \(45^\circ\)
• w,h = 384, 288
• standardna devijacija pogreške: jedan piksel, \(\sigma\) = 1.00

Osnovni postupak

Ispitni program treba za svaki pomak \(\theta\) provesti nexp = 100 eksperimenata nad uzorkom od szSample = 50 slučajnih parova točaka, rekonstruirati relativnu orijentaciju nenormaliziranim algoritmom s osam točaka te zabilježiti srednju kutnu pogrešku rekonstruiranog vektora translacije.

Hartleyeva normalizacija

Procijeniti doprinos Hartleyeve normalizacije te usporediti dvije varijante postupka na grafu točnost - pomak za pomak \(\theta \in [0, 10, 20, ..., 90]\) (stupnjevi).

Literatura: (hartley97pami)

Robusna estimacija (bonus)

Izmjeriti robusnost postava za \(\theta\) = \(90^\circ\) tako da se prikaže grafička ovisnost točnosti o udjelu uvedenih lažnih korespondencija. Točke lažnih korespondencija valja nasumično uzorkovati iz uniformne distribucije koja pokriva cijelu sliku.

Izmjerenu točnost osnovne metode treba usporediti s robusnom metodom utemeljenoj na konsenzusu slučajnog uzorka (RANSAC).

Literatura: (nister04pami).

Združena optimizacija (bonus)

Procijeniti doprinos združene optimizacije relativne orijentacije kamera i strukture scene.

Literatura: (engels06isprs), (jeong10cvpr).